我们知道db就是概率的游戏,也正是一些奇特的db结果引起了数学家帕斯卡(Pascal)和大数学家费马(Fermat)的兴趣,他们通过信件交流,提出了一些概率论的原理,从而创立了概率论。今天我们就来介绍几个db中的概率趣题,告诉我们的道理就是,就算打赌,也要精“打”细算。 完美的dbNBA球队湖人队和小牛队有一场比赛,两个队都有的忠实粉丝,就叫他们“人族”和“牛族”吧。粉丝当然都觉得自己支持的球队更可能赢球,所以愿意跟你打赌。假设“人族”认为湖人赢的概率为 p,“牛族”认为小牛赢的概率为 q ,p 和 q 都应大于50%。接下来就是有趣的部分了,我们总能很轻易就设计一个方法,分别与“人族”和“牛族”打赌,但不管结果如何,我们都稳赚不赔! 方法是这样的:我们分别与“人族”和“牛族”打一样的赌,如果我们赢了就得到 y 元,输了就失去 x 元,只要 y>x 我们就赚了。而 x 和 y 只需要满足下面两个简单的不等式,“人族“和”牛族“的期望收益为正,就会跟我们打赌: p * x - ( 1-p ) * y > 0q * x - ( 1-q ) * y > 0加上 y>x 的限制,画出的图像就是三条直线所包围的区域,对于里面的任意一点的坐标值(x,y)就是一个必胜方案。如果p>q, 解就是下图中的蓝色部分: 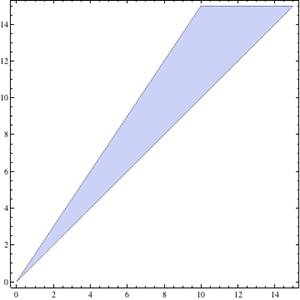 看来这个问题是完美地解决了,可是还有一个疑点,相信读者很快就能发现它的荒谬所在:不管“人族”还是“牛族”,他们的期望收益都是正的,也就是说,长久地看,他们都会赚钱,而我们又是稳赚不亏的,那么多出来的钱是哪里来的呢,怎么可能每个人都赚钱呢?
三张卡片的骗局这是另一个巧妙的赌局,我们先准备有三张卡片,1号卡片正反面都是黑色,2号卡片正反面都是红色,3号卡片一面是黑色,一面是红色。然后把卡片放进一个盒子里,摇一摇,让对手抽一张平放在桌子上。接着和他赌反面的颜色和正面一样。这个赌局看起来是公平的,比如抽到一张表面是黑色的卡片,那么卡片不是1号就是3号,反面的颜色不是黑色就是红色,直觉上概率各占1/2。 事实上我们赢的概率不是1/2,而是2/3,这个赌局最迷惑人的地方是卡片的“两面性”。玩家抽的不是3张牌,而是6个面:3个黑面,3个红面。我们把这6个面编上号A、B、C、D、E、F:  当玩家抽到黑面时,也就是A、C、D三种等可能的情况,它们的背面则分别是D、F、A,黑色的情形占了2/3。 这个问题最早于1889年由法国数学家伯特纳(Joseph Louis François Bertrand)提出,因为这个问题的结果出人意料,它又被称为“伯特纳箱悖论(Bertrand's box paradox)”。1950年美国数学家沃伦•韦弗(Warren Weaver)介绍了上面的卡片玩法,马丁•加德纳(Martin Gardner)称之为“三张卡片的骗局(three-card swindle)”。
如此不平凡的黑桃A有时候我们赌博一开始会放水,先让别人赚些小钱,放长线钓大鱼,最后来个一网打尽。下面就是一个绝佳的范例。四个人在打桥牌,我先说:“来打个赌吧,我现在有一张A,你们猜猜我还有没有更多A?”这种情况下你很可能会输,这时你在心里默默指定一个花色的A,比如说黑桃A,当某一轮抓到一张黑桃A后,这时机会就来了:“再打一个赌吧,我现在有一张黑桃A,你们猜猜我还有没有更多的A?” 很多人肯定觉得两个赌根本没什么不同的嘛,加了个黑桃并不要紧。可它们间的区别,大到令人不敢相信。我们就先算算第一次赌的概率吧: 没有A的情形:C(48,13)至少有1张A的情形:C(52,13)-C(48,13)恰好有1张A的情形:4*C(48,12)至少有2张A的情形:C(52,13)-C(48,13)-4*C(48,12)事件X为至少有两张A,事件Y为至少有一张A,那么条件概率为: P(X|Y)=P(XY)/P(Y)=(C(52,13)-C(48,13)-4*C(48,12))/(C(52,13)-C(48,13))≈37% 这个时候我要赌自己还有A,比较容易输掉。但是有了第一个赌的铺垫之后,大家打赌的意愿都被调动起来了,一看第二个赌不就是换了身衣服嘛,纷纷加大赌注,接着赌我没有更多A,正中我们下怀。下面我们将发现第二个赌的概率已经大大不同: 有黑桃A的情形:C(51,12)没有其它A的情形:C(48,12)还有其它A的情形:C(51,12)-C(48,12)事件X为还有其它A,事件Y为有黑桃A,条件概率为: P(X|Y)=P(XY)/P(Y)=(C(51,12)-C(48,12))/C(51,12)≈56%。 掌握了概率论,赌博就只是概率游戏了,当然我们是反对欺骗的,以上各种游戏只建议在朋友间进行以活跃气氛。还有一点很关键,打赌的时候,演得逼真点,别让他们知道你是传说中的死理性派!
|